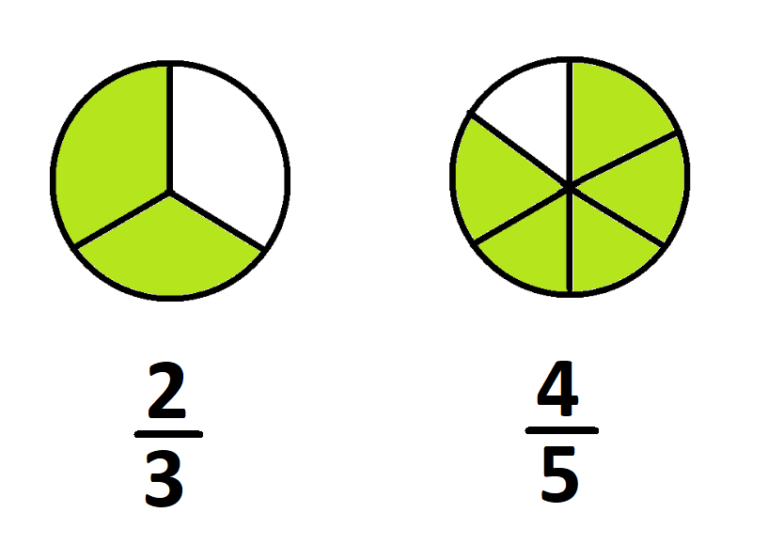
✅ Para crear fracciones fácilmente, divide un todo en partes iguales. Usa el numerador para las partes deseadas y el denominador para el total de partes. ¡Simplicidad garantizada!
Para hacer fracciones de manera sencilla y rápida, primero debes entender que una fracción se compone de dos números: el numerador (el número de arriba) y el denominador (el número de abajo). Para crear una fracción, simplemente coloca un número en el numerador y otro en el denominador. Por ejemplo, si tienes 3 manzanas y las quieres compartir entre 4 amigos, la fracción sería 3/4.
Ahora bien, en este artículo profundizaremos en los pasos para realizar fracciones de forma más eficiente. Veremos temas como la simplificación de fracciones, la suma y resta de fracciones, así como la multiplicación y división. Además, te ofreceremos ejemplos prácticos que te ayudarán a comprender mejor cada uno de estos procesos.
1. ¿Qué es una fracción?
Una fracción representa una parte de un todo. Se utiliza para expresar una cantidad que se divide en partes iguales. Por ejemplo, si tienes una pizza que se corta en 8 porciones y comes 3, puedes decir que has comido 3/8 de la pizza. Las fracciones pueden ser:
- Propias: cuando el numerador es menor que el denominador (ej. 1/2).
- Improprias: cuando el numerador es mayor o igual al denominador (ej. 5/4).
- Mixtas: combinan un número entero con una fracción (ej. 1 1/4).
2. Simplificación de fracciones
La simplificación de fracciones es un proceso esencial para hacerlas más manejables. Para simplificar una fracción, busca el máximo común divisor (MCD) de los números que forman el numerador y el denominador. Por ejemplo, si quieres simplificar 8/12, el MCD de 8 y 12 es 4. Por lo tanto, divides ambos números por 4 y obtienes 2/3.
Ejemplo de simplificación:
Fracción original: 24/36
MCD: 12
Fracción simplificada: (24 ÷ 12) / (36 ÷ 12) = 2/3
3. Suma y resta de fracciones
Para sumar o restar fracciones, es necesario que tengan el mismo denominador. Si no lo tienen, debes encontrar un denominador común. Por ejemplo, para sumar 1/4 + 1/6, el denominador común es 12:
- Convierte las fracciones: 1/4 = 3/12 y 1/6 = 2/12.
- Realiza la suma: 3/12 + 2/12 = 5/12.
4. Multiplicación y división de fracciones
Para multiplicar fracciones, simplemente multiplica los numeradores entre sí y los denominadores entre sí. Por ejemplo, para multiplicar 2/3 x 4/5:
- Numeradores: 2 x 4 = 8
- Denominadores: 3 x 5 = 15
- Resultado: 8/15
Para dividir fracciones, multiplica la primera fracción por el inverso de la segunda. Por ejemplo, para dividir 3/4 ÷ 2/5:
- Inverso de 2/5 es 5/2.
- Multiplica: 3/4 x 5/2 = 15/8.
Ejemplos prácticos para entender las fracciones paso a paso
Entender las fracciones puede ser una tarea desafiante, pero con ejemplos prácticos y un enfoque metódico, se puede hacer más sencillo. A continuación, presentaremos algunos ejemplos que ilustran cómo realizar operaciones con fracciones de manera efectiva y comprensible.
Ejemplo 1: Sumar fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, simplemente sumamos los numeradores y mantenemos el mismo denominador. Por ejemplo:
- Fracción 1: 2/5
- Fracción 2: 1/5
Para sumarlas:
2/5 + 1/5 = (2 + 1)/5 = 3/5
Ejemplo 2: Restar fracciones con diferentes denominadores
Para restar fracciones con diferentes denominadores, primero buscamos un denominador común. Consideremos:
- Fracción 1: 3/4
- Fracción 2: 1/2
El denominador común entre 4 y 2 es 4. Convertimos la segunda fracción:
1/2 = 2/4
Ahora podemos restar:
3/4 – 2/4 = (3 – 2)/4 = 1/4
Ejemplo 3: Multiplicar fracciones
La multiplicación de fracciones es sencilla: multiplicamos los numeradores y luego los denominadores. Veamos el siguiente ejemplo:
- Fracción 1: 2/3
- Fracción 2: 3/5
La multiplicación se realiza de esta forma:
(2 × 3)/(3 × 5) = 6/15
Si simplificamos, obtenemos:
6/15 = 2/5
Ejemplo 4: Dividir fracciones
Para dividir fracciones, multiplicamos por el inverso de la segunda fracción. Consideremos:
- Fracción 1: 1/2
- Fracción 2: 3/4
El cálculo sería:
1/2 ÷ 3/4 = 1/2 × 4/3 = (1 × 4)/(2 × 3) = 4/6
Si simplificamos, obtenemos:
4/6 = 2/3
Consejos prácticos para trabajar con fracciones
- Practica con ejemplos: Cuanto más practiques, más fácil se te hará entender las fracciones.
- Haz uso de diagramas: Visualizar las fracciones con dibujos o diagramas puede facilitar su comprensión.
- Utiliza herramientas: Calculadoras en línea pueden ser útiles para verificar tus respuestas.
Recuerda que entender las fracciones es un proceso gradual. Con cada paso, ganarás más confianza y destreza en el manejo de estas importantes herramientas matemáticas.
Preguntas frecuentes
¿Qué son las fracciones?
Las fracciones representan una parte de un todo, expresadas como un número dividido por otro.
¿Cómo se suman fracciones?
Para sumar fracciones, necesitas un denominador común. Luego, sumas los numeradores y mantienes el denominador.
¿Qué es un denominador común?
Es un número que puede ser usado como denominador para dos o más fracciones, facilitando su operación.
¿Cómo se simplifican las fracciones?
Para simplificar, divides el numerador y el denominador por su máximo común divisor (MCD).
¿Qué son las fracciones impropias?
Son aquellas donde el numerador es mayor o igual que el denominador, representando un número mayor a uno.
¿Cómo se multiplican fracciones?
Multiplicas los numeradores entre sí y los denominadores entre sí, simplificando el resultado si es necesario.
| Punto Clave | Descripción |
|---|---|
| Fracciones | Representan una parte de un todo, se expresan como a/b. |
| Denominador | El número que se encuentra abajo en la fracción. |
| Numerador | El número que se encuentra arriba en la fracción. |
| Suma de fracciones | Requiere un denominador común. |
| Multiplicación de fracciones | Multiplicamos los numeradores y denominadores. |
| Simplificación | Reducir la fracción dividiendo por el MCD. |
| Fracciones mixtas | Combinan un número entero con una fracción. |
¡Deja tus comentarios y cuéntanos qué te pareció! No olvides revisar otros artículos de nuestra web que también podrían interesarte.